綺麗に撮れるカメラとは
2015/03:発行
2020/03:更新
2020/03:更新
目次
2-4. フルサイズはなぜボケ易いのか?
撮像素子と画角の関係を分かって頂いた所で、次はいよいよポートレートで最も重要な背景のボケについて考えてみます。
今更述べる必要もないでしょうが、ポートレートの撮影においては、被写体を綺麗に浮き立たせるために、いかにして綺麗に背景をボカスかが鍵になります。
しかしながらこのボケに関して、大きな撮像素子ほど大きなアドバンテージがあるのです。
逆に言えば、小さな撮像素子ほどボケを作るのが難しいのです。
これは、撮像素子の小さなスマホで撮った写真がボケ難い事から既に十分認識されていると思います。
この理由は、撮像素子が小さくなる写る範囲が狭くなるので、(同じ焦点距離のレンズで撮ると)被写体が大きくなってしまいます。
このため、小さな撮像素子のカメラで被写体をフルサイズと同じ大きさで撮るためには、広角系のレンズを使用する必要があり、広角系のレンズを使うと必然的に被写界深度が深くなってしまうからです。
恐らくこう説明してもすんなりご理解頂けないと思いますので、これからもう少し詳しく且つ分かり易くご説明したいと思います。
と言いながら、一部計算式まで載せていますので、難しい所はどんどん飛ばして、読んで頂ければと思います。
1) フルサイズとAPS-Cサイズの写りの違い
それでは最初に、同じ場所から同じ135mm F2.0のレンズを使って、フルサイズとAPS-Cサイズのカメラで撮った2枚の写真を見て下さい。

今回は画角ではなく、ボケに注目して下さい。


フルサイズ(135mm F2.0) APS-Cサイズ(135mm F2.0)
画角が変わる事で被写体同様にボケも拡大されていますが、被写体に対するボケ具合は同じだと思われますよね。
何しろ(既にお気付きの様に)、上の右側の写真は左の写真の中央部を抜き出しただけなのですから。
フルサイズであってもAPS-Cサイズであっても、同じレンズで同じ絞りを使えば、画角(写る広さ)は変わるものの同じ様なボケ効果を得る事は可能なのです。
あれ、でもついさっき撮像素子が小さいとボケ難いと言ったじゃない、と思った方はその通りです。
何故ならば、APS-Cサイズのカメラに135mm F2.0のレンズを付けている限り、絶対に左の様な写真は撮れないからです。
ですので、話は更に続きます。
2) 被写体を同じ大きさにしたらどうなるか
上の写真の様に画角が異なる状態では、両者とも同じボケですが、両者を正しく比較するためには、当然同じ条件にして比較する必要があります。
すなわち、APS-Cサイズのカメラで、(左上の写真と同じ様に)人物を同じ大きさで撮影して比較しなければなりません
という訳で、APS-Cサイズカメラのレンズを換えて、左の写真の様に写してみましょう。
そのためには、もともと使っていた135mmレンズの画角が18度なので、APS-Cサイズのカメラで画角18度になるレンズを使用しなくてはなりません。
これはレンズの仕様書を調べなくても分かります。
キヤノンの場合、フルサイズ対応レンズの焦点距離を1.6(正確には撮像素子の対角線比で1.617ですがここでは簡単に1.6で計算します)で割れば、APS-Cサイズで同じ画角になるレンズの焦点距離が分かります。
なお本書では、この1.6を換算係数と呼ぶ事にします。
ですので、85mm(135÷1.6=84.3)のレンズを使って、同じく絞りをF2.0にして同じ場所から撮影してみましょう。
フルサイズで画角18度 APS-Cサイズで画角18度
さて左上の写真と同じ様になるでしょうか?

モデルが人相の悪いノラ猫で恐縮ですが、上の写真の様にボケは同じにはなりません。
なぜならば、85mmのレンズの方が、135mmの方よりも広角側ですので、同じF2.0の絞りだと85mmの方がボケ難いからです。
3) APS-Cサイズで同じボケになる様にするにはどうするか
では85mmのレンズで絞りをいくつにすれば同じボケが得られるのでしょう。
F1.8でしょうか、それともF1.2でしょうか、或いは中間のF1.4でしょうか?

多少専門的な話になりますが、ボケの量はレンズの有効口径に比例します。
有効口径は焦点距離を開放絞り値で割れば算出できますので、135mm F2.0のレンズの場合、有効口径は以下の様に67.5mmなります。
| 有効口径 | = | 焦点距離÷絞り値 |
| = | 135mm÷2.0 | |
| = | 67.5mm |
とすると、85mm(正確には84.3mm)で有効口径が67.5mmになる様にするには、絞り値は以下の様にF1.25になります。
| フルサイズと同じボケ量となる絞り値 | = | 焦点距離÷有効口径 |
| = | 84.3mm÷67.5mm | |
| = | 1.25 |
同じ画角で同じボケ量になる絞り値
余談ながら、ここで耳寄りな話をさせて下さい。
上の二つ式をまとめると、以下の様になります。
| フルサイズと同じボケ量となる絞り値 | = | 焦点距離÷有効口径 |
| = | (焦点距離÷1.6)÷(焦点距離÷2.0) | |
| = | (135mm÷1.6)÷(135mm÷2.0) | |
| = | 2.0(F値)÷1.6(換算係数) | |
| = | 1.25 |
何が言いたいかと言えば、フルサイズと同じボケ量を得るには、フルサイズの絞り値を単に換算係数の1.6で割るだけで求められるという事です。
そして、もしフルサイズと同じ画角で同じボケ量の写真を撮るには、焦点距離を1.6で割ったレンズを使って、絞りも1.6で割った値にセットすれば良い事になります。
後ほどこれを使った表をお見せしますので、覚えておいて頂ければと思います。
そして下が85mm F1.2で撮った写真ですが、おおよそ同じボケになる事が分かって頂けると思います。

すなわち、F2.0より2倍明るい85mm F1.4でも足らず、2.6倍(2.02÷1.252=4÷1.59=2.56)明るいF1.25のレンズを使えば、理論的に同じボケが再現できるという訳です。
これを絞りの段数(AV値)に変換すると以下の式(エクセル関数でも表記)の様に、1.3段(1+1/3段階)となります。
絞り段数(AV)= log2 2.56= LOG(2.56,2)= 1.36
これをさらに図示化すると以下の様になります。

生憎85mmでF1.25のレンズは市販されていないのですが、以下のアマゾンの広告にもあります様に、その上の85mm F1.2のレンズを見る限りかなり高価なのは間違いありません。
135mm F2.0 85mm F1.8 85mm F1.2
すなわち、小さな撮像素子のカメラで、それより大きなサイズの撮像素子のカメラと同じ画角で同じボケ効果を出すのは、かなり難しいという事を分かって頂けましたでしょうか。
キヤノンのAPS-Cサイズに関するお話
さてここまでは、キヤノンのAPS-Cサイズを例にしてお話ししてきました。
ところが、キヤノンのAPS-Cサイズは、他社(ニコン、ソニー等)のAPS-Cサイズより若干小さいのです。
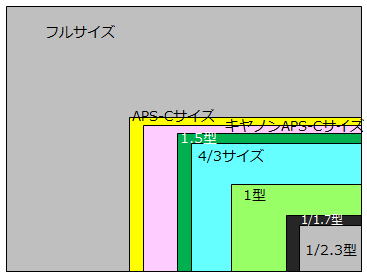
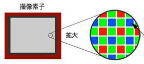
撮像素子の大きさの比較
このため、他社製のAPS-Cサイズとフルサイズの違いについてもお伝えしておきます。
【サイズ】
先ずサイズの違いですが、他社のAPS-Cサイズは23.6x15.6㎜なのに対して、キヤノンは22.2x14.8mmしかなく、他社のAPS-Cサイズを100%とするとキヤノンのそれは88%しかないのです。
【焦点距離】
このため、他社製APS-Cサイズ機でフルサイズの135㎜レンズと同じ画角に対応するレンズは、90㎜(=135÷1.5)になります。
【絞り】
ですので、90mmで有効口径が67.5mmになる様にするには、絞り値はF1.33(=90/67.5)になります。
キヤノンの絞り値はF1.25でしたので、これを図で表すと以下の様になります。
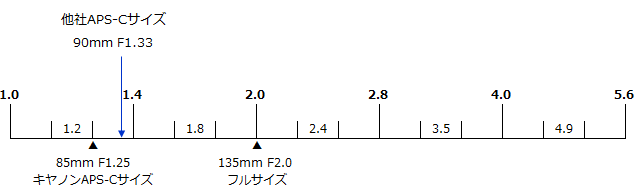
また、フルサイズのF2.0と明るさを比較すると2.25倍(22/1.332=4/1.78=2.25)となり、やはりキヤノンの2.6倍と僅かに異なります。
更にこれをAV値にすると1.2段で、キヤノンの1.3段と異なるのですが、1/3ステップで表示すれば、いずれも1+1/3段階になります。
このため本書におきましては、キヤノンのAPS-Cサイズを例に述べていますが、その他一般のAPS-C サイズとは多少異なります事ご容赦願います。
4) 焦点距離の相関表
次にフルサイズと同じボケを作るためには、どれくらいの明るさのレンズが必要かカメラ一眼の種類(撮像素子のサイズ)毎に見てみたいと思います。
でもその前に、フルサイズと同じ画角にするために、焦点距離の相関表をお見せしておきましょう。
| No. | FULL | APS-C | APS-C (キヤノン) |
4/3 | 1インチ | 1/2.3 |
| 1 | 24 mm | 16 mm | 15 mm | 12 mm | 9 mm | 4 mm |
| 2 | 35 mm | 23 mm | 22 mm | 18 mm | 13 mm | 6 mm |
| 3 | 50 mm | 33 mm | 31 mm | 25 mm | 18 mm | 9 mm |
| 4 | 85 mm | 56 mm | 52 mm | 43 mm | 31 mm | 15 mm |
| 5 | 100 mm | 65 mm | 62 mm | 50 mm | 37 mm | 18 mm |
| 6 | 135 mm | 88 mm | 83 mm | 68 mm | 50 mm | 25 mm |
| 7 | 180 mm | 118 mm | 111 mm | 90 mm | 66 mm | 33 mm |
| 8 | 200 mm | 131 mm | 123 mm | 100 mm | 73 mm | 36 mm |
| 9 | 300 mm | 196 mm | 185 mm | 150 mm | 110 mm | 54 mm |
| 10 | 400 mm | 262 mm | 247 mm | 200 mm | 147 mm | 73 mm |
| 変換係数 | 1.000 | 0.654 | 0.617 | 0.500 | 0.367 | 0.182 |
細かい説明は不要とは思いますが、例えば一般的なAPS-Cサイズのカメラを使って、フルサイズの135mmと同じ画角で撮影したい場合は、88mmのレンズを使う必要があります。
また4/3サイズのカメラで50mmのレンズを使うと、フルサイズの100mmの画角と同じになります。
なお表の一番下に焦点距離の変換係数を載せておきました。
ですので、もしフルサイズの85mmを1インチサイズに変換したければ、85mmに0.367を掛けて31mmとなります。
逆に1インチサイズの13mmをフルサイズに変換したければ、13mmを0.367で割って35mmになります。
5) 絞りの相関表
お待たせしました。
いよいよフルサイズと同じボケを作るための、絞りの相関表です。
下の表は、フルサイズを基準として、撮像素子の異なるカメラに同じ画角のレンズを取り付けて、同じ様にボカスのに必要な絞り値を示しています。
| FULL | APS-C | APS-C (キヤノン) |
4/3 | 1インチ | 1/2.3 |
| F 1.0 | F 0.7 | F 0.6 | F 0.5 | F 0.4 | F 0.2 |
| F 1.2 | F 0.8 | F 0.7 | F 0.6 | F 0.4 | F 0.2 |
| F 1.3 | F 0.8 | F 0.8 | F 0.6 | F 0.5 | F 0.2 |
| F 1.4 | F 0.9 | F 0.9 | F 0.7 | F 0.5 | F 0.3 |
| F 1.6 | F 1.1 | F 1.0 | F 0.8 | F 0.6 | F 0.3 |
| F 1.8 | F 1.2 | F 1.1 | F 0.9 | F 0.7 | F 0.3 |
| F 2.0 | F 1.3 | F 1.2 | F 1.0 | F 0.7 | F 0.4 |
| F 2.3 | F 1.5 | F 1.4 | F 1.2 | F 0.8 | F 0.4 |
| F 2.6 | F 1.7 | F 1.6 | F 1.3 | F 0.9 | F 0.5 |
| F 2.8 | F 1.8 | F 1.7 | F 1.4 | F 1.0 | F 0.5 |
| F 3.3 | F 2.1 | F 2.0 | F 1.6 | F 1.2 | F 0.6 |
| F 3.7 | F 2.4 | F 2.3 | F 1.8 | F 1.3 | F 0.7 |
| F 4.0 | F 2.6 | F 2.5 | F 2.0 | F 1.5 | F 0.7 |
ちなみにこの表はどうやって作ったかと言うと、上段の”同じ画角で同じボケ量になる絞り値”で述べました様に、例えばキヤノンのAPS-Cサイズの場合、フルサイズの絞り値を1.6で割って求めています。
この表をご覧頂きます様に、例えばフルサイズと同じ画角のレンズを使って、フルサイズのF1.4のボケを作るためには、APS-Cサイズの場合F0.9のレンズが必要になります。
焦点距離も一緒にお伝えすると、フルサイズの50mm F1.4と同じボケを出すためには、APS-Cサイズでは33mm F0.9のレンズが必要という事です。
更には4/3サイズのカメラで、フルサイズのF1.4のボケを作るためにはF0.5と、とんでもなく明るいレンズが必要になります。
また現実的な話をすると、フジフィルムにAPS-Cサイズ用の56mm F1.2(9万4千円)という高級レンズがありますが、これはフルサイズ用に換算すると85mm F1.8(4万3千円)と普及レンズ並みのボケになるという事です。
56mm F1.2 APS-C |
85mm F1.8 Full |
85mm F1.8 Full |
更にオリンパスから今後F1.0のレンズが発売されると噂されていますが、それとてもフルサイズのF2.0のボケにしかならないという訳です。
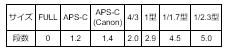
なお上の表を更に簡素化したものが、以下になります。
| サイズ | FULL | APS-C | APS-C (Canon) |
4/3 | 1型 | 1/1.7型 | 1/2.3型 |
| 段数 | 0 | 1.2 | 1.4 | 2.0 | 2.9 | 4.4 | 4.9 |
フルサイズを基準とした同じ被写界深度となる絞りの段数
段数で表示していますので、絞り値と直接リンクしませんが、絞りの相対差は分かり易いかもしれません。
6) 後に下がって撮ったらどうなるか
それでは次に、フルサイズとAPS-Cサイズのカメラで同じ大きさで被写体を撮る別の手を、お話ししておきましょう。
APS-Cサイズカメラで上半身まで撮影するもう一つの方法として、レンズはそのままで、今撮影している場所から更に後ろに下がる手もあります。(この場合画角が変わりますので、背景の写る範囲が異なります)
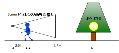
後ろに下がれば、当然被写体との距離が離れます。
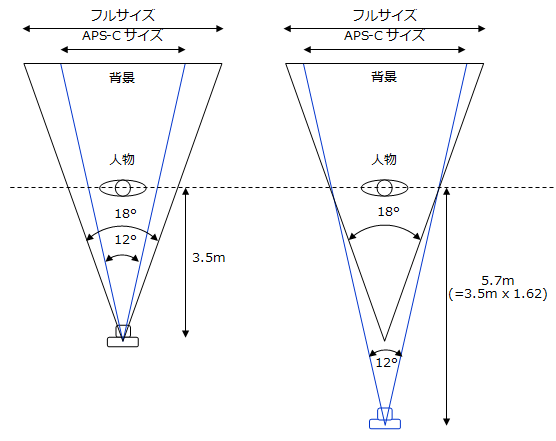
上の図の様に、フルサイズとAPS-Cサイズのカメラに135mmレンズを付けて撮影したときの被写体までの距離が3.5mだとすると、APS-Cサイズのカメラに同じレンズを付けて、フルサイズで撮ったのと同じ大きさで被写体が入る様にするのには、1.62(変換係数)倍の5.7m被写体から離れなくてはいけません。
被写体と離れるとどうなるかと言うと、被写体深度が深くなってやはり背景がボケ難くなるのです。
いきなり被写体深度という難しい言葉が出てきましたが、要はレンズの特性として、近い物にピンとを合わせると背景はボケ易くなり、遠い物にピントを合わせると背景がボケ難くなるのです。
大雑把な計算値ですが、この場合のボケ量の減りは絞りで1+2/3段階分に相当します。
すなわち元々は135mm F2.0のレンズだったのですが、後に下がる事により、背景のボケはF3.7に絞ったのと同じくらいに低下したという事です。
ですから、APS-Cサイズのカメラでレンズを換えたり、後ろに下がったりしても、フルサイズと同じボケ効果を出すのは非常に難しいのです。
ただしです、前段でお話しました様に、被写体をアップ気味に撮っておけば、フルサイズと同じ様なボケ効果を得る事ができるという事は覚えておいて下さい。
7) まとめ
本項をまとめると、以下の様になります。
撮像素子の小さなカメラで、背景をボカスのは難しい。
ただし、被写体に近付く(被写体をアップで撮る)事によってボケ効果を期待できる。
ところで、スマートフォンの様にかなり小さな撮像素子になると、いくら近付いても背景までしっかりピントが合ってしまいます。
この場合、記念写真には最適なものの、ポートレートには全く向きませんので、もしポートレートを綺麗に撮りたいならば、少しでも大きな撮像素子を使ったカメラを別に購入するしかありません。
少し余談になるかもしれませんが、実は35mmフルサイズよりもっと大きな撮像素子を使うデジタルカメラは存在します。


Hasselblad H5D-60 フェーズワン645DF
この様なカメラを使うと背景はおろか、油断すると被写体すらボケてしまう程です。
かなり長文になってしまいましたが、お分かり頂けたでしょうか?
2-5. ポートレートに適した撮像素子とは
それでは最後にポートレートに最適な撮像素子について考えてみたいと思います。
それに際して、各項のまとめを見てみましょう。
1)撮像素子が大きくなれば必然的に画素数は増え、画像は高精細になり綺麗に見える。
かと言って、いたずらに高画素を求める必要はない。
2)撮像素子が小さくなると、望遠レンズで撮ったのと同じ様な画像になる。
ただしレンズを換える事で、(撮像素子が小さくても)同じ画角の写真を撮る事は可能である。
3)撮像素子の小さなカメラで、背景をボカスのは難しい。
ただし、被写体に近付く(被写体をアップで撮る)事によってボケ効果を期待できる。
いかかでしょう。
これらを見る限り、1)と2)についてはポートレートにとって然程重要ではないと言えます。
という訳で、本章の最終まとめとしては以下の様にしたいと思います。
もし背景をぼかしたポートレートを撮りたいのならば、なるべく大きなサイズの撮像素子を搭載したカメラが理想である。
撮像素子について分かった所で、次にカメラの構造の違いについて考えてみたいと思います。