背景を定量的にぼかす5つの方法
2016/5: Issue
2017/3: Renewal
2019/5: Correction
2017/3: Renewal
2019/5: Correction
2021/1: Renewal
目次
はじめに
写真の楽しさを知ってくると、次に挑戦したくなるのが前景や背景のボケたちょっとお洒落な写真ではないでしょうか。

SONY α7S FE 85mm F1.4 GM F1.7 1/2000秒 ISO100
確かに上の写真の様に背景がボケると、単に被写体を浮き上がらせるだけではなく、何とはなしに吹き寄せる穏やかで爽やかな空気すら感じます。
そう思ってカメラ雑誌を読めば、決まって以下の様に書かれています。
背景をぼかす方法
①絞りを開ける。
②望遠系レンズを使う。
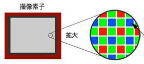
③撮像素子の大きなカメラを使う。
④被写体に近づく。
⑤被写体から背景を離す。
ですが、同じレンズで1絞り開けるのと、レンズの焦点距離を2倍にするのでは、どちらがボケ易いのでしょうか?
また被写体までの距離を半分にすると、どれだけ背景がボケるのでしょうか?
またフルサイズのカメラとAPS-Cサイズのカメラでは、どの程度ボケの大きさが違うのでしょうか?
従来の解説書では、そういった定量的(具体的)な説明が一切ありませんでした。
このため本書におきましては、これらの疑問を一掃すべく、ボケの大きさを計算で求めて、サンプル写真とイラストとチャートと数値を駆使して、背景を定量的にぼかす方法を理論的に且つ分かり易くご説明してみたいと思います。
2. 結論
それではお忙しい方のために、先に結論を述べておきましょう。
背景を定量的にぼかす方法は以下の通りです。
背景を定量的にぼかす方法
①絞りを1段開けると、ボケの大きさは1.4倍になる。
(ボケの大きさは絞り値に反比例する)
②レンズの焦点距離を2倍にすると、ボケの大きさは4倍になる。
③撮像素子の大きさ(長さ比)を2倍にすると、ボケの大きさは2倍になる。
④被写体までの距離を半分にすると、ボケの大きさは2倍になる。
⑤背景を無限遠にすると、ボケは最大になる。
なお、ここで言う所のボケの大きさとは、点光源のボケの直径と思って頂ければと思います。
この点光源のボケが組み合わさって、背景がボケて見えると言う訳です。
ではなぜこう言えるかについては、これからじっくりご説明します。
3. 絞りとボケの関係
それでは最初に、絞りを開けるとどのくらいボケるのかをお伝えしたいと思います。
既に前項でお伝えしています様に、非常に簡単なのです。
絞りを1段開けると、ボケの大きさは1.4倍になり、絞りを2段階開けると、ボケの大きさも2倍になるのです。
これをグラフで表すと以下の様になります。
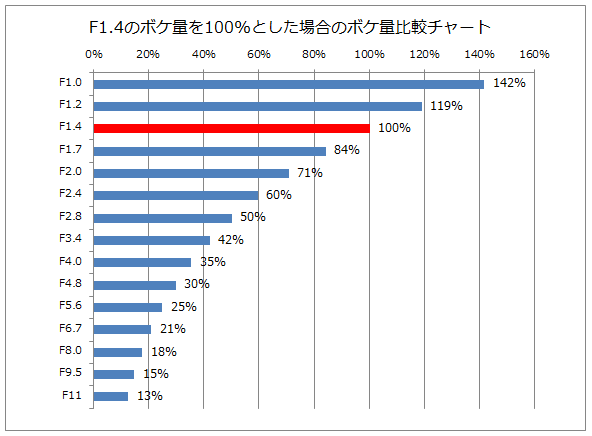
これはF1.4のボケの大きさを100%にした場合の、各絞りのボケ量を表しています。
これをご覧頂きます様に、F1.4に対してF2.0のボケ量は1/1.4の71%、F2.8のボケ量は1/2の50%になります。

絞りをf2.8からf1.4にするとボケの直径は2倍になる
なぜそう言えるかにつきましては、ボケの大きさは以下の式で計算できるからです。
| ボケの大きさ(直径)=(焦点距離)2× 1/絞り値 × |1/被写体までの距離-1/背景までの距離| |
なおここで言うボケの大きさ(ボケ量)とは、背景にある点光源のボケの直径を指します。
それでは次にこのボケ量を写真で見てみましょう。

絞りとボケの関係を表すサンプル写真
上の写真は、フルサイズのカメラに85mm F1.2のレンズを装着して、同じ被写体と背景を絞りを変えて撮った写真です。
ちなみにカメラから被写体までの距離が1m、被写体から背景までが4mほどです。
この写真の①と③の写真を見比べて頂くと、①の背景にある点光源のボケの直径が③の2倍の大きさになっているのを分かって頂けると思います。
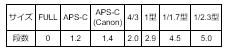
①は絞りf1.2で、③は絞りf2.4ですので、下の表の様の様に段数にすれば2段階分絞りを開いた事になります。
| 段数 | 0 | 0.5 | 1.0 | 1.5 | 2.0 | 2.5 | 3.0 | 3.5 | 4.0 |
| 絞り値 | 1.0 | 1.2 | 1.4 | 1.8 | 2.0 | 2.4 | 2.8 | 3.5 | 4.0 |
また①の絞りf1.2と②絞りf1.8のボケの大きさを比べると、①の方が1.4倍(正確には√2倍)ボケが大きくなります。
これで、絞りを1段階開けるとボケの直径は1.4倍、絞りを2段階開けるとボケの直径は2倍大きくなるという事をご理解頂けたと思います。
4. レンズの焦点距離とボケの関係
それでは次に、レンズの焦点距離を換えたらボケの大きさはどうなるかご説明します。
実はこれはびっくりで、レンズの焦点距離が2倍になると、ボケの大きさは4倍にもなるのです。
これも先の式で説明でき、もし焦点距離以外の値が同じであれば、ボケの大きさは焦点距離の2乗に比例する事になります。
| ボケの大きさ(直径)=(焦点距離)2× 1/絞り値 × |1/被写体までの距離-1/背景までの距離| |
ですので、下の図の様に同じ場所から焦点距離50mmのレンズと100mmのレンズを比べれば、同じ絞りでも100mmのレンズの方が背景のボケの直径が4倍になります。
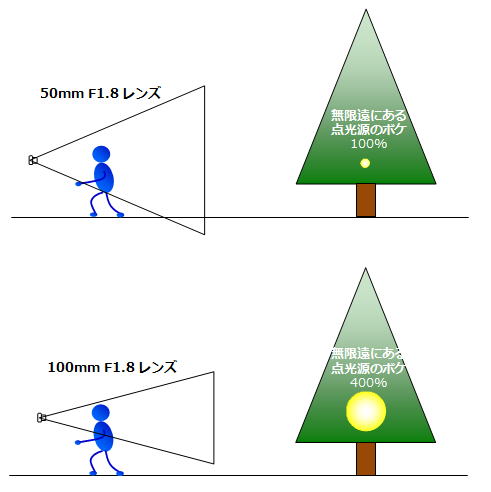
レンズの焦点距離が2倍になると、ボケの大きさは4倍にもなる
更に下のチャートの様にボケの大きさは放物線を描き、200mmになると16倍、300mmになると36倍、500mmレンズでは何と100倍になるのです。
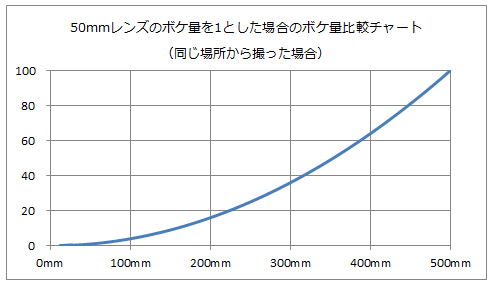
と、一般的な解説書はこれで終わるのですが、本書は違います。
なぜならば、同じ位置から同じ被写体と背景をレンズの焦点距離を変えて取ると、確かにボケは4倍に大きくなるのですが、被写体の大きさ自体も変わってしまい、全く異なる写真になってしまうからです。
ですので、ポートレートを考慮して背景のボケ量を比較するのでしたら、被写体の大きさを同じにして、背景のボケの大きさを比較しなければなりません。
例えば、もし50mmのレンズと同じ大きさで被写体を撮るのでしたら、100mmレンズの場合、被写体から更に2倍後ろに下がって撮らなければなりません。
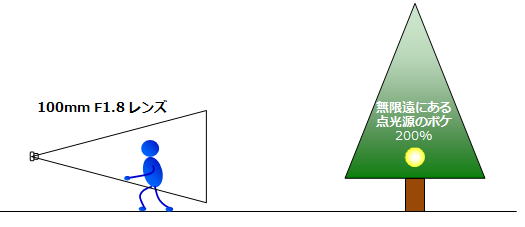
被写体から2倍離れると、ボケの大きさは半分になる
この場合、被写体から2倍離れる事になりますので、ボケの大きさは半分になります。
なぜそうなるかについては、後ほど6. 被写体までの距離とボケの関係にてご説明します。
では、そうやって撮影した写真を見比べてみましょう。
と言いたい所なのですが、生憎丁度良いサンプル画像が無いので、先ほど画像を流用してご説明したいと思います。

先ず、上の写真の赤字を見て下さい。
これは、元々のレンズである85mm f1.2に対して、②~③についてはそれぞれのボケの大きさになるレンズの焦点距離を計算で求めています。
これをご覧頂きます様に、①の85mm f1.2に対して、ボケの大きさが半分になる③の写真の場合、背景が無限遠の場合は42.5mm f1.2ですが、この条件下では37mmのレンズに相当します。
逆に言うと、同じ条件下において、37mm f1.2レンズにおける背景のボケを2倍にしたい場合、倍の焦点距離である74mm f1.2のレンズより更に望遠の85mm f1.2のレンズを使う必要がある、という事です。
と言う訳で、もし被写体の大きさを同じにして、無限遠にある背景のボケを2倍にしたいのらば、焦点距離が2倍のレンズを使えば良いと言えます。
これをグラフで表すと以下の様になります。
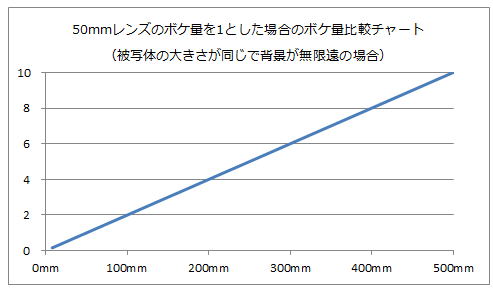
ただしもし背景が無限遠より近い場合は、2倍以上の焦点距離のレンズが必要になるという訳です。
ちなみに被写体から背景までの距離が10mの場合は、以下の様になり、背景が無限遠の場合より半分程度に小さくなります。
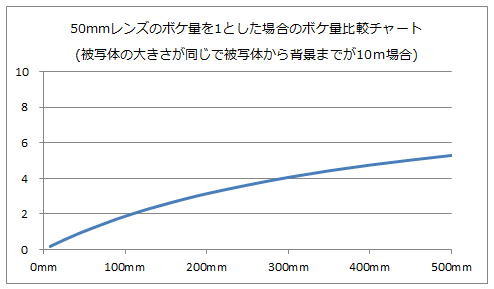
これでレンズの焦点距離とボケの関係を、ご理解頂けましたでしょうか。
なお上の写真は、あくまでも流用ですので、もし本当にレンズの焦点距離を変えて撮影した場合、レンズが広角になるほど被写体にデフォルメ(変形)が生じますし、背景の写る範囲も広くなります。
いつか機会があったら、正確なサンプル画像を撮ってみたいと思いますので、期待しないでお待ち下さい。
5. 撮像素子の大きさとボケの関係
それでは次に、撮像素子の大きさとボケの大きさについて考えてみます。
ご存じの様に撮像素子の大きさが変わると同じ焦点距離でもレンズの画角が変わりますので、これも画角を統一して比較しなければなりません。
ちなみに、小サイズ撮像素子からフルサイズへの焦点距離の変換係数は以下の様になります。
| 種類 | 対角線比 | 変換係数 | 85mm換算 |
| フルサイズ | 100% | 1倍 | 85mm |
| APS-Cサイズ | 65% | 1.5倍 | 56mm |
| APS-Cサイズ(Canon) | 62% | 1.6倍 | 53mm |
| 4/3サイズ | 50% | 2倍 | 42.5mm |
| 1インチサイズ | 37% | 2.7倍 | 32mm |
と思っていたら、丁度うまい具合に画角と開放絞り値の同じポートレート用のレンズが、各撮像素子のサイズで売られていますので、この4本比較してみる事にします。
Canon Fuji Film Panasonic Nikon
フルサイズ APS-Cサイズ 4/3サイズ 1インチサイズ
85mm F1.2 56mm F1.2 42.5mm F1.2 32mm F1.2
フルサイズ APS-Cサイズ 4/3サイズ 1インチサイズ
85mm F1.2 56mm F1.2 42.5mm F1.2 32mm F1.2
下の写真がその4本のレンズで開放で撮った写真です。

これまたどこかで見た事があるなと言うのは置いといて、これをご覧頂きます様に、フルサイズが最もボケが大きく、①~④の順番で徐々にボケが小さくなるのが分かって頂けると思います。
このボケの大きさをグラフで表すと以下の様になります。
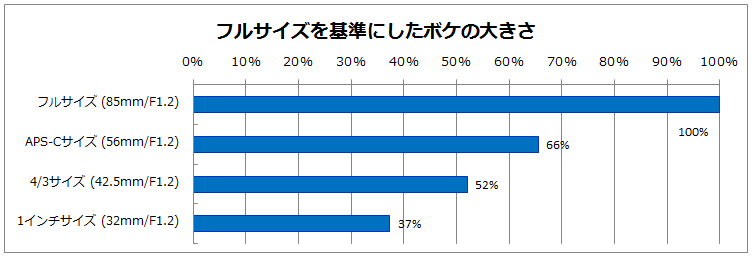
チャート1(被写体まで2m、被写体から背景まで4m)
このグラフを見て、おっと思われたかたはいらっしゃいませんでしょうか?
もし気が付かれた方は、かなりカメラに詳しいか、本書をしっかりお読み頂いた方です。
棒グラフの横にフルサイズを基準にしたパーセントが書かれていますが、この値は撮像素子のサイズ比率(正確には対角線比)に極めて近似しているのです。
| 種類 | 対角線比 | 変換係数 | 85mm換算 |
| フルサイズ | 100% | 1倍 | 85mm |
| APS-Cサイズ | 65% | 1.5倍 | 56mm |
| APS-Cサイズ(Canon) | 62% | 1.6倍 | 53mm |
| 4/3サイズ | 50% | 2倍 | 42.5mm |
| 1インチサイズ | 37% | 2.7倍 | 32mm |
近似していると書きましたが、数値が多少ずれているのは、撮像素子のサイズがフルサイズの様にピッタリ3:2ではないせいですので、理論的にはボケ量は撮像素子のサイズに比例すると思って頂いて構いません。
誤解している方が多いので何度も書きますが、ボケの大きさは撮像素子の大きさに比例するのです。
これで撮像素子の大きさとボケの関係を明確にご理解頂けたと思います。
おっと忘れていました。
既にお気付きの通り、このサンプル画像もいつもの写真の流用で、やはり計算で撮像素子のサイズを求めています。
これについてはこちらで詳しく述べていますので、もしお暇でしたら覗いてみて下さい。
6. 被写体までの距離とボケの関係
次は被写体までの距離とボケの関係を見てみましょう。
今までは顔をメインにしたショルダーアップの写真でしたが、次に少し離れてバストアップのポートレートはどうなるか見てみましょう。
これを見ると、ちょっとびっくりの結果ではないでしょうか。

ご覧の様に、ほんの1~2歩下がっただけなのに、こんなにも背景のボケが小さくなりました。
念のために、今までの写真を載せておきましょう。

勿論背景と被写体までの距離は同じなのですが、先ほどの写真と見比べると違いは一目瞭然で、被写体も小さくなると共に、背景のボケも一気に小さくなりました。
最初の写真に対して、ほんの数m後ろに下がっただけで、これだけボケの効果が失われてしまうのです。
特に⑦⑧においては、ほとんどボケと呼べないくらいになっています。
以前お伝えしました様に、もし背景が無限遠にあるとしたら、被写体から2倍離れるとボケの大きさは半分になります。
これについても以下の式で説明が付きます。
| ボケの大きさ(直径)=(焦点距離)2× 1/絞り値 × |1/被写体までの距離-1/背景までの距離| |
先ず背景までの距離が無限遠ですと、”1/背景までの距離”は、1を無限で割る事ですので、ゼロになります。
となると、残るのは”1/被写体までの距離”だけですので、もし他の焦点距離や絞り値が同じであれば、ボケの大きさは被写体までの距離に反比例すると言えます。
ちなみに、被写体から背景までの距離を4mとした場合の、被写体までの距離とボケの大きさの関係をグラフで表すと以下の様になります。
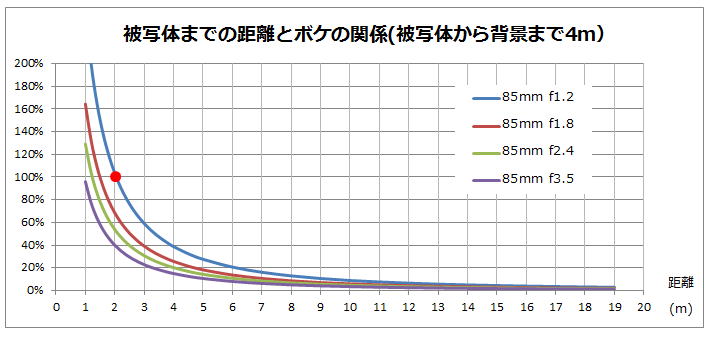
チャート3
このチャートは、絞りf1.2で被写体までの距離が2mのときのボケ量を100%として、被写体までの距離を変えるとボケの大きさがどう変化するかを表しています。
これをご覧頂きます様に、被写体までの距離を3m以内にすると、急激にボケが大きくなるのに対して、被写体から6m以上離れると、ボケの大きさが20%以下になっているのが分かります。
もし背景をぼかしたいのならば、積極的に被写体に近づく事が重要であり、ある程度離れてしまうと殆どボケは期待できなくなってしまう、と言えます。
7. 背景までの距離とボケの関係
それでは最後に、背景までの距離とボケの関係を見てみましょう。
今回はサンプル写真が無いので、先に背景までの距離が無限遠の場合のチャートをお見せしましょう。
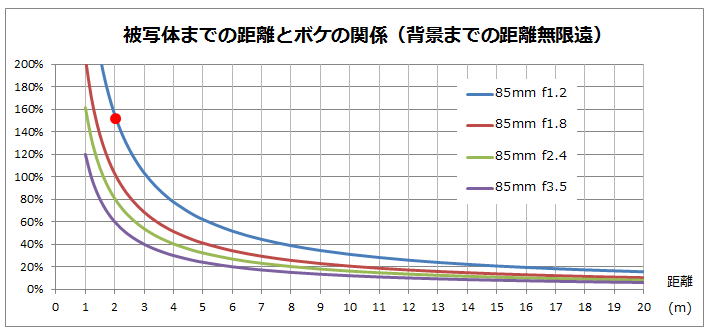
チャート4
これを先ほどのチャートと比べると、違いが良く分かって頂けると思います。

チャート5
先ほどの背景が被写体までが4mの場合と比べると、赤点の位置が100%から155%になりますので、大よそ5割増しでボケが大きくなったと言えます。
また先ほどは、被写体までの距離が6mを超えるとボケ量は20%以下になったのですが、背景が無限ですと16mまで伸びています。
これで、背景が被写体から遠ざかればボケが大きくなる事をご理解頂いたと思います。
それでは次に、にこのチャートもお見せしておきましょう。
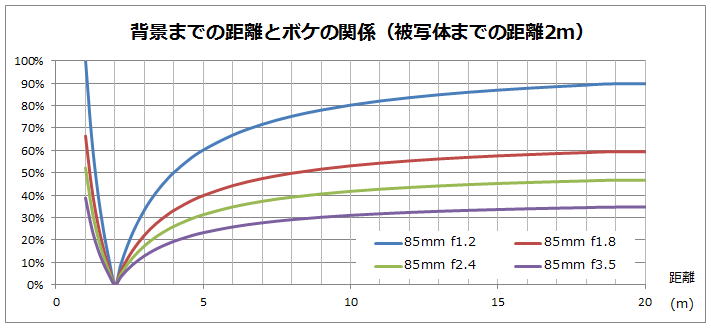
チャート6
今までは、被写体から背景までの距離が2mと無限遠の場合だけで話をしてきましたが、このチャートは被写体から背景までの距離が徐々に変わるとボケの大きさがどう変化するを表しています。
これをご覧頂きます様に、背景を大きくぼかすためには背景までの距離を8m以上、最低でも3m以上確保するのが望ましいと言えます。
また被写体から近い場合はボケの大きさが急激に変化するのに対して、遠い場合はさほどボケに影響しない事が分かります。
ですので、背景を大きくぼかすには、被写体から背景までの最初の数メートルが重要だと言えます。
8. 遠くのボケと近くのボケ
それではここで、面白い事をお伝えしましょう。
先ほど背景が遠いほどボケが大きくなるとお伝えましたが、奇妙な事に気が付いた方はいらっしゃいませんでしょうか?
もう一度、前項のチャートを見て下さい
被写体までの距離が2mで、背景がそれから4mの場合のボケの大きさが100%で、背景が無限遠の場合のボケの大きさが155%になっています。
変ではありませんか?
通常でしたら、手前にある物が大きく写り、奥にある物のほど小さく写ります。
にも関わらず、前出のチャートによれば、奥にあるボケの方が大きくなると言っているのです。
ものは試しで、実際にどうなるか写真で見てみましょう。

カメラに近い点光源(赤)より遠い点光源(白)の方がボケは大きくなる。
上の写真は手前が赤い光源、奥が白い光源なので、絞りを思いっきり絞って、手前と奥の光源にピントを合わせれば、手前の赤い光源の方が当然大きく写ります。(85mm f16の写真参照)
ところが、絞りを徐々に開けて光源がボケていくと、あら不思議。
なんと、大きさが逆転して、奥の白の光のボケが、手前の赤いボケより大きくなっているのが分かります。
この場合、赤の光源はカメラから2m、白い光源はカメラから6mほど離れた所にあります。
これから更に白い光源だけ後に下げると、白のボケはもっと大きくなり、計算上では赤いボケの2倍まで大きくなります。
ちなみに下の写真はライブハウスのステージを、わざとぼかして撮った写真です。

点光源が無限遠に近くなるとボケの大きさは変わらない
これを見ると下にある赤系の光源の方が、上にあるブルー系の光源より手前にある様に見えますが、実際は奥にあるのです。
ちなみに下の光源は、ステージ上のドラムとギターの反射で、上の光源はそれより手間に飾られた電飾です。

ボケの大きさは、前後で逆転する。
覚えておいて損は無いと思います。
9. 背景は明るく
最後にボケに関してもう一つ重要な事をお伝えしなければなりません。
それはぼかす背景は、なるべく明るいものでなければいけないという事です。
例えば下の写真の場合、多少明るい部分があるのでボケてもまだ許せるのですが、これが曇り空で暗めの背景になると途端に見苦しいボケになってしまいます。

暗い背景がボケると見苦しい
ですのでもし背景をぼかしたいのでしたら、下の写真の様になりべく明るい背景を選ぶ事をお薦め致します。

明るい背景がボケると美しい
特にボケが大きいと、何気ない風景でも意外にお洒落な背景になったりします。
10. まとめ
いかがでしたでしょうか。
まとめると以下の様になります。
①絞りを2段階開けると、ボケの大きさも2倍になる。
②レンズの焦点距離が2倍になると、ボケの大きさは4倍になる。
ただし被写体の大きさを同じにして背景のボケ量を2倍にしたい場合は、2倍以上の焦点距離のレンズを使う必要がある。
③ボケの大きさは、撮像素子の大きさに比例する。
④被写体に近付くと急激にボケがが大きくなるが、ある程度離れてしまうと殆どボケは期待できなくなってしまう。
⑤背景が被写体から遠ざかればボケが大きくなるが、重要なのは最初の数メートルである。
⑥ボケが綺麗なのは、明るい背景の場合である。
本書がお役に立てば幸いです。