クロップしたらボケの大きさはどうなるのか
2020/06:発行
2020/11/15:更新
2020/11/15:更新
目次
1. はじめに
カメラの解像度が上がった事に伴い、クロップをして撮像素子に写った画像の一部を抜き出して使用する機会が多くなってきました。
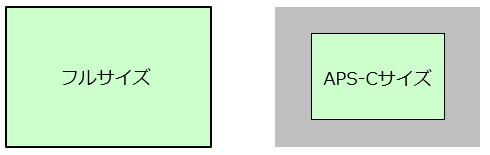
フルサイズとAPS-Cサイズの比較(長さ比で1.5:1)
例えば、下左の写真はフルサイズ機に85mm F1.4の明るい単焦点レンズを付けて開放で撮ったもので、右はその時にAPS-Cサイズにクロップした写真です。

FE 85mm F1.4 GM 絞り開放撮影 APS-Cクロップ(130mm相当/絞りは?)
と言いたい所ですが、実はフルサイズの写真を後でAPS-Cサイズにトリミングしたものです。
ただし、全く同じなのでここではクロップしたという事にしておいて下さい。
これをご覧頂きます様に、クロップすると元の写真に対して望遠レンズで撮った様な写真になります。
具体的には、オリジナルのレンズの焦点距離である85mmを焦点距離の換算係数である1.5倍した130mm(正確には128mm)の望遠レンズで撮ったのと同じ画角になるのは、何方もご存知の事でしょう。
それでは、ボケ(被写界深度)はどうなるのでしょうか?
130mm F1.4のレンズで撮った写真と同じボケになるのでしょうか?
今回はその謎に迫ってみたいと思います。
2. 結論
それではいつもの通り、先に結論をお伝えしておきましょう。
先ほどお見せした写真は、お伝えしました様に85mm F1.4のレンズを使って開放で撮影していますが、これをAPS-Cサイズにクロップした場合、130mm のレンズをF2.1で撮った写真と同じボケ(被写界深度)になります。
単純に考えると、APS-Cサイズにクロップすれば、ボケも拡大されるので、130mmのF1.4で撮ったのと同じボケになると思ってしまいますが、実際はそれよりボケは小さくなってしまうのです。
では、このF2.1と言う値はどうやって求めたかと言うと、下の式にあります様に、元々の絞り値であるF1.4に、APS-Cサイズへの焦点距離の換算係数である1.5を掛けただけなのです。
クロップした場合の絞り値=元の絞り値×換算係数
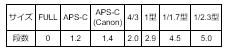
ちなみに、フルサイズをAPS-Cサイズ以外にクロップした場合の換算係数(対角線比)は以下の様になります。
| サイズ | FULL | APS-C (注) |
APS-C (Canon) |
1.5型 | 4/3 | 1型 | 1/1.7型 | 1/2.3型 |
| 換算係数 | 1.0 | 1.5 | 1.6 | 1.9 | 2.0 | 2.7 | 4.6 | 5.5 |
フルサイズをクロップした場合の換算係数
注:APS-Cサイズはメーカーによってバラつきがありますが、ここでは代表値として1.5(実際は1.52~1.56)としておきます。
ですので、先ほどの写真を仮にマイクロ4/3サイズにクロップしたら、レンズの焦点距離は170mm(=85×2)になり、絞りはF2.8(=1.4×2)で撮ったのと同じボケ(同じ写真)になります。
またクロップから少々話がずれてしまいますが、もしAPS-Cサイズのカメラをお使いの方でお手持ちのレンズの開放値がF1.2だとしたら、それはフルサイズで同じ画角のF1.8(=1.2×1.5)相当のボケ量(被写界深度)のレンズになるという訳です。
XF56mm F1.2 (APS-Cサイズ) |
E 85mm F1.8 (フルサイズ) |
同じ画角のAPS-CサイズのF1.2とフルサイズのF1.8とは同じボケ量になる
3. 計算式の解説
それでは、なぜ元のレンズの絞り値に換算係数を掛ければ、クロップした場合の絞り値が求められるかご説明します。
なお計算と聞いただけで寒気がする方は、気持よく本項をスキップして次項に飛んで頂いて結構です。
先ず、ボケの大きさは、レンズの有効口径に比例します。
そして、有効口径は焦点距離を絞り値で割れば算出できます。
ですので、元のレンズの有効口径は以下の式で求められます。
| 元の有効口径 | = | 元の焦点距離÷元の絞り値 |
次にAPS-Cサイズにクロップしたレンズの有効口径は、以下の式で求められます。
| クロップの有効口径 | = | クロップの焦点距離÷クロップの絞り値 |
この元のレンズの有効口径とクロップしたレンズの有効口径が同じになれば、両者のボケが同じ大きさになりますので、以下の式が成り立ちます。
| 元の焦点距離÷元の絞り値 | = | クロップの焦点距離÷クロップの絞り値 |
上の式よりクロップしたレンズの絞り値は、以下の様に求められます。
| クロップの絞り値 | = | クロップの焦点距離÷(元の焦点距離÷元の絞り値) |
| = | (クロップの焦点距離×元の絞り値)÷元の焦点距離 |
ここで、クロップしたレンズの焦点距離は、元のレンズの焦点距離に換算係数を掛ければ求められますので、これを上の式に代入すれば以下の様になります。
| クロップの絞り値 | = | クロップの焦点距離×元の絞り値/元の焦点距離 |
| = | ( |
|
| = | 元の絞り値×換算係数 |
すなわち、元のレンズと同じボケ量になるAPS-Cサイズにクロップしたレンズの絞り値は、元のレンズの絞り値に換算係数を掛ければ求められるという事です。
説明が長くなってしまいましたが、ご理解頂けましたでしょうか。
4. 検証
それでは、実際にそうなるかどうか、検証してみましょう。
なお生憎、上記条件にピッタリ合うレンズの持ち合わせがないため、代わりに24-105mm F4.0のズームレンズを使ってみます。
また使用するカメラがキヤノン機のため、APS-Cサイズの換算係数は1.6になります。
使う焦点距離はズーム内ならどこでも良いのですが、例えば105mmは66mmの1.6倍ですので、66mmで撮った写真をAPS-Cサイズにクロップすれば、105mmで撮った写真と同じになる筈です。
そう思って撮った写真が、以下になります。

66mm F4.0で撮った写真 66mm F4.0をAPS-Cサイズにクロップした写真
これは被写体までの距離が0.7mで、後方の光源が被写体から4mほど後方にあります。
ご覧の様にクロップした写真は、被写体もボケ量もオリジナルより1.6倍大きくなっています。
こうなると、105mm F4.0で撮った写真とボケ量は同じになると、誰もが思ってしまうでしょう。
では、このクロップした写真を、実際に105mm F4.0で撮った写真と比べてみます。

66mm F4.0をAPS-Cサイズにクロップした写真 105mm F4.0で撮った写真
すると、どうでしょう。
背景の光源は、実際に105mm F4.0で撮った方が明らかにボケが大きいのが分かって頂けると思います。
それでは次に、F4.0に1.6を掛けたF6.4で撮った写真と比べてみます。

66mm F4.0をAPS-Cサイズにクロップした写真 105mm F6.4で撮った写真
するとご覧いただきます様に、計算通り背景のボケの大きさはほぼ同じになりました。
なおボケの大きさが僅かに違って見えるのは、正確に絞りF6.4や焦点距離66mmに合わせられなかったためとご理解願います。
ついでにフルサイズをクロップすると、どれくらいボケが小さくなるのかを段数(EV値)で表したのが、以下の表になります。
| サイズ | FULL | APS-C | APS-C (Canon) |
4/3 | 1型 | 1/1.7型 | 1/2.3型 |
| 段数 | 0 | 1.2 | 1.4 | 2.0 | 2.9 | 4.4 | 4.9 |
フルサイズを基準とした同じ大きさのボケになる絞りの段数
これをご覧頂きます様に、例えば今回の様にフルサイズをキヤノンのAPS-Cサイズにクロップした場合、同じ画角のレンズを使っても1.4段絞った(F4.0→F6.4)のと同じボケの大きさになるという訳です。
またクロップするサイズが小さい程、ボケも小さくなるのが分かります。
5. まとめ
それでは、まとめです。
①クロップ機能を使うと、望遠レンズで撮ったのと同じ効果が得られるが、ボケ量は実際に望遠レンズを撮った場合よりも小さくなる。
②このため、もし同じボケ量の写真を撮りたいのであれば、元のレンズの絞り値に換算係数を掛けた絞り値に設定すれば可能である。
なおついでにお伝えしておきますと、(はじめにでもお伝えしました様に)クロップは後で写真をトリミングしたのと同じです。
ですので、本書としましては(どうしてもファイル容量を小さくしたいのでなければ)撮影時はフルサイズで撮っておく事をお勧めします。
クロップしたらボケの大きさはどうなるのか