デュアルスロットにするとメモリー不良のリスクはどれくらい軽減されるのか?
2018/11/13:発行
1. はじめに
カメラのメモリーが壊れて、撮った写真が消えてしまった。
誰しも青ざめる瞬間です。
そんなとき、デュアルスロットのカメラにすれば良かったとか、誰しも思うものです。

Nikon D850のデュアルスロット
確かに複数のメモリーがあれば、いざというときに有効なのは間違いありません。
ですが、その場合の故障率は1台と比べてどれくらい下がるのでしょうか?
限りなくゼロに近付くのでしょうか?
今回はその謎に迫ってみようと思います。
故障率とは
という訳で、早速簡単な例で考えてみましょう。
故障率とは、ある装置が稼働した場合、何時間に1回故障するかを表し、以下の式で求めます。
故障率=故障回数÷稼働時間
ですので、ある装置の故障率が1回/100時間だとしたら、100時間稼働したら(計算上)その間のどこかで1回は必ず故障するという事になります。
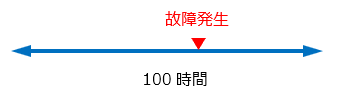
それでは心配なので、同じ装置を2台用意して、同じ様に稼働させたら全体の故障率はどうなるでしょう。
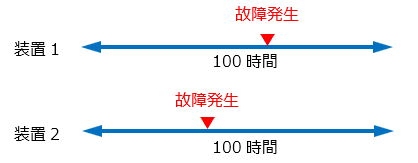
単純に考えると、0.5回/100時間になりそうな気もするのですが、それも変です。
なぜならば、0.5回/100時間という事は、200時間に1回故障する事になります。
ですが、上の図の様にどちらの装置も100時間に1回は必ず故障するとしたら、故障の間隔が200時間に1回になるとも思えません。
かと言って、せかっく装置を2台にしたのですから、故障率が1回/100時間より小さくなるのは間違いないでしょう。
となると、何となく全体の故障率は、1回/100時間と1回/200時間の間にある様な気がしますが、それ以上は手詰まりです。
もしかしたら、そんな事は確率を使えば簡単に求められると思われるかもしれませんが、それは無理です。
何故ならば、上記した故障率は(長さや重さの様に)時間の単位を持った絶対値であって、一般的な単位の無い”率”を表しているのではないからです。
もっと分かり易く言えば、サイコロを振って1が出る確率は、1/6(=1回/6回)でこれには単位がありません。
ですので、この場合は確率の計算が可能なのですが、1回/100時間の様に単位が付いていると確率の計算はできないのです。
故障率を確率に変換する
そんな時はどうするか?
不本意ながら、計算できるものに変換するしかありません。
今回の場合でしたら、時間の単位が付いた故障率を、単位の付かない本当の”率”に変換します。
信頼度
そこで登場するのが、信頼度です。
信頼度とはある期間tの間に1回も故障しない確率の事で、以下の式で求められます。
信頼度R=e-λ(故障率)x t(時間)
この式でなぜ信頼度を求められるかは専門書を見て頂くとして、これは非常に便利な式ですので、ぜひこの機会に覚えて頂ければと思います。
例えば、故障率が1回/100時間で、使用時間が1時間だとすると、信頼度は以下の様になります。
| 信頼度R | =e-λ(故障率)x t(時間) |
| =e-1回/100時間 x 1時間 | |
| =e-1/100 | |
| =0.9901 |
すなわち、故障率が1回/100時間の装置を1時間使うだけなら、この間99.0%の確率で問題なく(故障する事なく)使えるという事です。
逆に言えば、故障率が1回/100時間の装置を1時間使うと、故障が発生する確率が1%あるという事です。
ちなみにもし2時間使うと信頼度は96%、10時間使うと信頼度は90%、50時間使うと60%、100時間使うと37%、そして200時間使うと14%にまで落ちます。
これをグラフにすると以下の様になります。
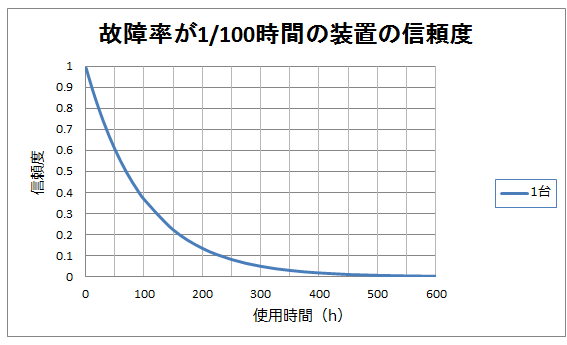
これをご覧頂きます様に、450時間を過ぎた辺りから信頼度は1%以下になり、ほぼ確実に故障が発生すると言えます。
ちなみに今回お話しました信頼度は、”ある期間tの間に1回も故障しない確率”の事でしたので、不良率(何時間に1回故障するかの率)とは意味合いが異なります。
ですので、もし”ある期間tの間に1回以上故障する確率”を知りたいのでしたら、1から信頼度を引けば簡単に求められます。
例えば上記の様に信頼度が90%だとしますと、不信頼度(ある期間tの間に1回以上故障する確率)は10%になります。
装置が2つの場合の信頼度
お待たせしました。
それではいよいよ、同じ装置が2つになった場合の信頼度を求めてみましょう。
これは確率ですから、求めるのは簡単です。
例えば、1個のサイコロを振って1が出たら故障が発生したとします。
そして信頼度とは故障しない確率ですので、1から1/6を引いた5/6がサイコロ1個の信頼度と言えます。
そしてサイコロが2つある場合、両方とも1が出ると故障となり、その場合の確率は1/6 ×1/6で1/36になります。
そしてその信頼度は、1から1/36を引いた35/36になります。
これを応用して、2つの装置の故障率が1回/100時間で、使用時間が1時間だとすると、全体の信頼度は以下の式で求められます。
| 信頼度R | =1-(1-e-λ x t)x (1-e-λ x t) |
| =1-(1-e-1回/100時間 x 1時間)x (1-e-1回/100時間 x 1時間) | |
| =1-(1-e-1/100)x (1-e-1/100) | |
| =1-(1-0.990)x (1-0.990) | |
| =1-(0.01)x(0.01) | |
| =0.9999 |
すなわち、故障率が1回/100時間の装置を2台にすると、1時間使うだけなら、99.99%の確率で問題なく(故障する事なく)使えるという事になります。
先程の1台の場合の信頼度が99.01%でしたので、信頼度が増したのが分かります。
そして先程と同じ様に、これをグラフ化すると以下の様になります。
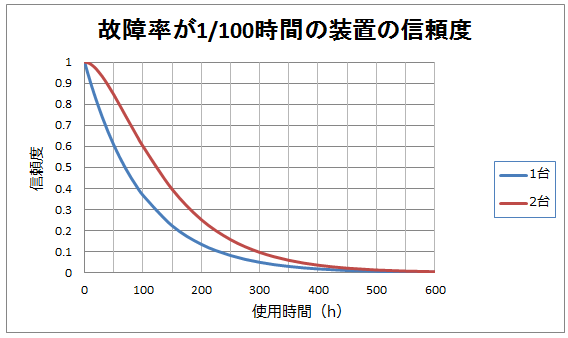
これをご覧頂く様に、装置を2台にすると全体的に信頼度が上がっているのが分かります。
例えば、使用時間が50時間を見てみると、信頼度が0.6から0.84に40%アップし、100時間では0.37から0.6へ62%アップしています。
とは言え、とんでもなく信頼度が上がるという訳ではない事は分かって頂けるのではないでしょうか。
信頼度の改善率
そんな訳で、次に装置が1台の場合と2台の場合で、信頼度が何%くらいアップしているかを計算して、先ほどのラフに載せてみます。
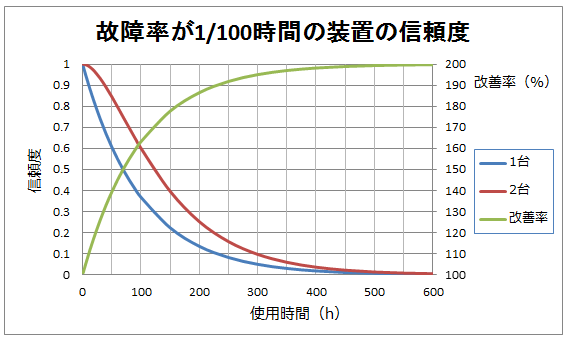
これをご覧頂きます様に、使用時間が長くなるに連れて、装置2台の信頼度は1台の場合よりどんどん200%(2倍)に近付いていくのが分かります。
ただし残念ながら、2倍以上になる事は決してありません。
また100時間以内で使っている場合、最大でも60%ほどしか信頼性はアップしません。
まとめ
さて、まとめです。
①同時に動く装置を2台にすれば、故障率(単位時間当たりの故障件数)が下がるのは間違いないが、故障率は(時間のディメンションのある)絶対値なので確率(計算)で求めるのは困難である。
②このため、信頼度(ある期間tの間に1回も故障しない確率)に変換して計算すると、使用時間が延びるにつれて、信頼度は2倍に近づいていく。(ただし、2倍以上になる事はない)
③ちなみに故障率が1回/100時間の装置の場合、信頼度が半分(50%)になるのは、1台の場合で70時間、2台の場合で120時間である。
本書がお役に立てば幸いです。
デュアルスロットにするとメモリー不良のリスクはどれくらい軽減されるのか?
Tweet
ご意見、ご感想等ありましたら是非こちらに。
Your response would be highly appreciated.

ホーム頁へ戻る
戻る
時代錯誤の親指AF次へ
ドットとピクセルの違いTweet
ご意見、ご感想等ありましたら是非こちらに。
Your response would be highly appreciated.

ホーム頁へ戻る