写真をトリミングした場合の画角の求め方

2020/05：発行

1. はじめに

カメラの解像度が上がった事に伴い、トリミングをして写真の一部を拡大して使用する機会が多くなってきました。

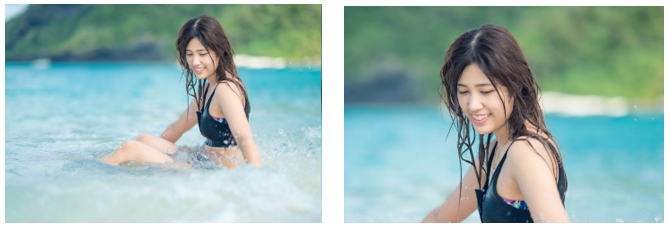
トリミングすれば、画角が変わり望遠レンズで撮ったのと同じ画像になるのは、どなたもご存知の事でしょう。

では、例えば撮った写真を2/3の大きさにトリミングしたら、画角はどれだけ変わるのでしょうか？

今回はその謎に迫ってみたいと思います。

2. 画角の変化

それでは先ず、画角の変化から考えてみます。

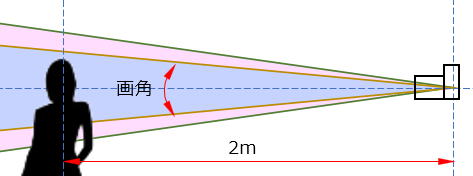
下の写真は、85mm F1.4のレンズを使って2m程離れた被写体を開放で撮っています。

85mm F1.4で撮った写真　　　　　　　　中央部分を2/3にトリミングした写真

そして右側の写真は、その中央の2/3部分を抜き出して拡大した写真になります。

本書ではこれを、2/3にトリミングした写真と呼び、2/3をトリミング率と呼ぶ事にします。

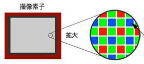
また撮像素子上でこの話をすると、左の写真が撮像素子の全域（36mm×24mm）に写った画像で、右の写真はその中央の24mm×16mの領域に写った画像と言えます。

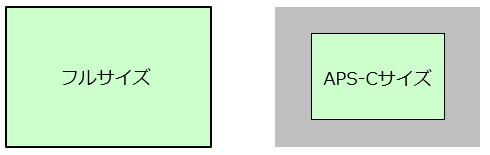
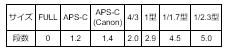
ちなみにこの2/3のトリミング率とは、（機種によって多少バラつきが有りますが）フルサイズをAPS-Cサイズにクロップしたのと同じ比率になります。

このため以降の説明は、フルサイズをAPS-Cサイズにクロップした場合と同じ、と思って頂ければと思います。

それでは次に、この条件でトリミングした場合の画角を、計算で求めてみます。

3. 画角の計算方法

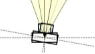
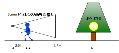
計算と聞くと、下の図の様に（レンズから）被写体側で考えてしまいますが、これですと不明な長さが多く簡単には求められそうにありません。

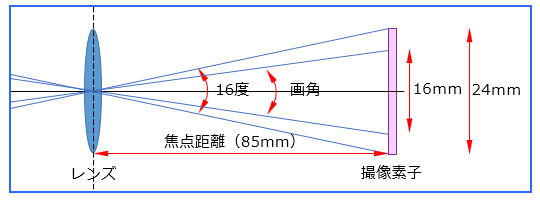
そんな訳で、下の図の様にレンズから後ろ側、すなわち撮像素子側の図を使って、2/3にトリミングした場合の画角を計算してみます。

学生時代に戻って、上図の画角を三角関数を使って計算すると以下の様になります。

画角	＝	（tan^-1（画像の長さ/2÷レンズの焦点距離）×180/Π）×2
	＝	（tan^-1（16/2÷85）×180/3.14）×2
	＝	11度（正確には10.８度）

なお上の式にあるΠとはパイ、すなわち円周率の事です。

また”画像の長さ”とは、撮像素子上におけるトリミング後の画像の長さになります。

この場合、フルサイズの撮像素子の高さ24ｍｍを2/3にトリミングしたので、16mmになります。

これによって、この場合の画角は11度というのが求められました。

ただし、上記のややこしい計算式は金輪際きれいに忘れて頂いて結構です。

本書がこれから、もっと現実的で実用的で簡単な画角の計算方法をお教えします。

4. 画角の簡易計算方法

その簡単な計算方法ですが、先ず焦点距離85mmの垂直方向の画角を調べます。

ネットで検索しても良いですし、もしお持ちでしたらレンズのカタログでも調べられます。

すると16度と書かれています。

次に、このの画角にトリミング率（ここでは2/3）を掛ければ求められるのです。

画角	＝	16度×2/3
	＝	11度（正確には10.7度）

上の計算結果をご覧の様に、これだけで先ほどと同じ11度の計算結果が得られます。

もしトリミング率が1/2であれば、画角は8度になります。

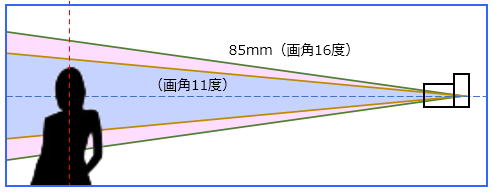
どうです、あっけないほど簡単でしょう。

この理由は、（三角関数を使わなくても）画角が狭いときは画像の高さは角度にほぼ比例するからです。

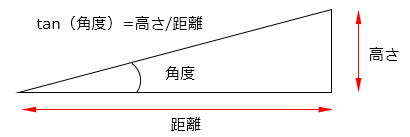
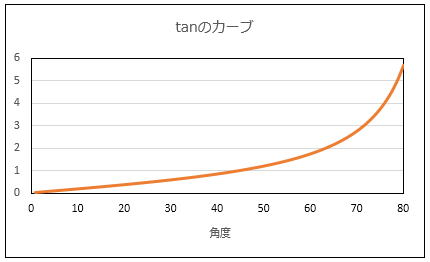
下はその高さと角度の関係を表すタンジェント（tan）のカーブですが、これをご覧頂きます様に70度を超えると一気にカーブが大きくなるものの、45度まではほぼ直線で、ぎりぎり60度までは何とか直線と見て良さそうな感じです。

ですので、角度が60度以内であれば、高さが半分になれば、角度も半分になるのです。

このため、今回の様に元が画角16度（60度以内）で、高さが2/3になったら、16度×2/3で画角は11度みなるという訳です。

なお、垂直方向の画角が60度を超える場合（20mmよりワイドな超広角レンズ）ですと誤差が大きくなってきますが、それより望遠側のレンズであればこの簡易計算方法が使えると思って頂いて結構です。

特に画角が45度以下になる35mm以上の望遠のレンズでしたら、誤差はほぼゼロになります。

覚えておいて損はありません。